这里记录了大一下学期的离散作业与答案,我会在每次作业截止后马上把我的答案放上来🐶🐶🐶
$$
\newcommand{\lfa}[0]{\leftrightarrow}\
\newcommand{\w}[0]{\wedge}\
\newcommand{\v}[0]{\vee}\
\newcommand{\an}[0]{\wedge}\
\newcommand{\o}[0]{\vee}\
\newcommand{\n}[0]{\neg}\
\newcommand{\a}[0]{\forall}\
\newcommand{\e}[0]{\exists}\
$$
第一次作业
$1.1$
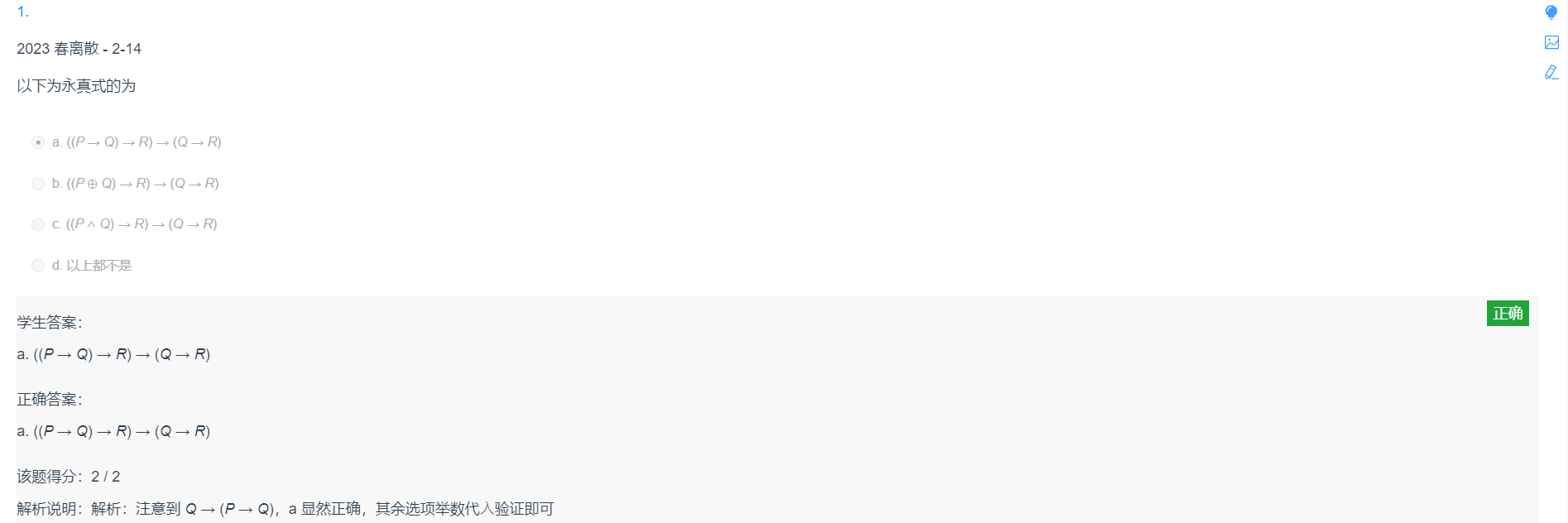
a
$2.1$
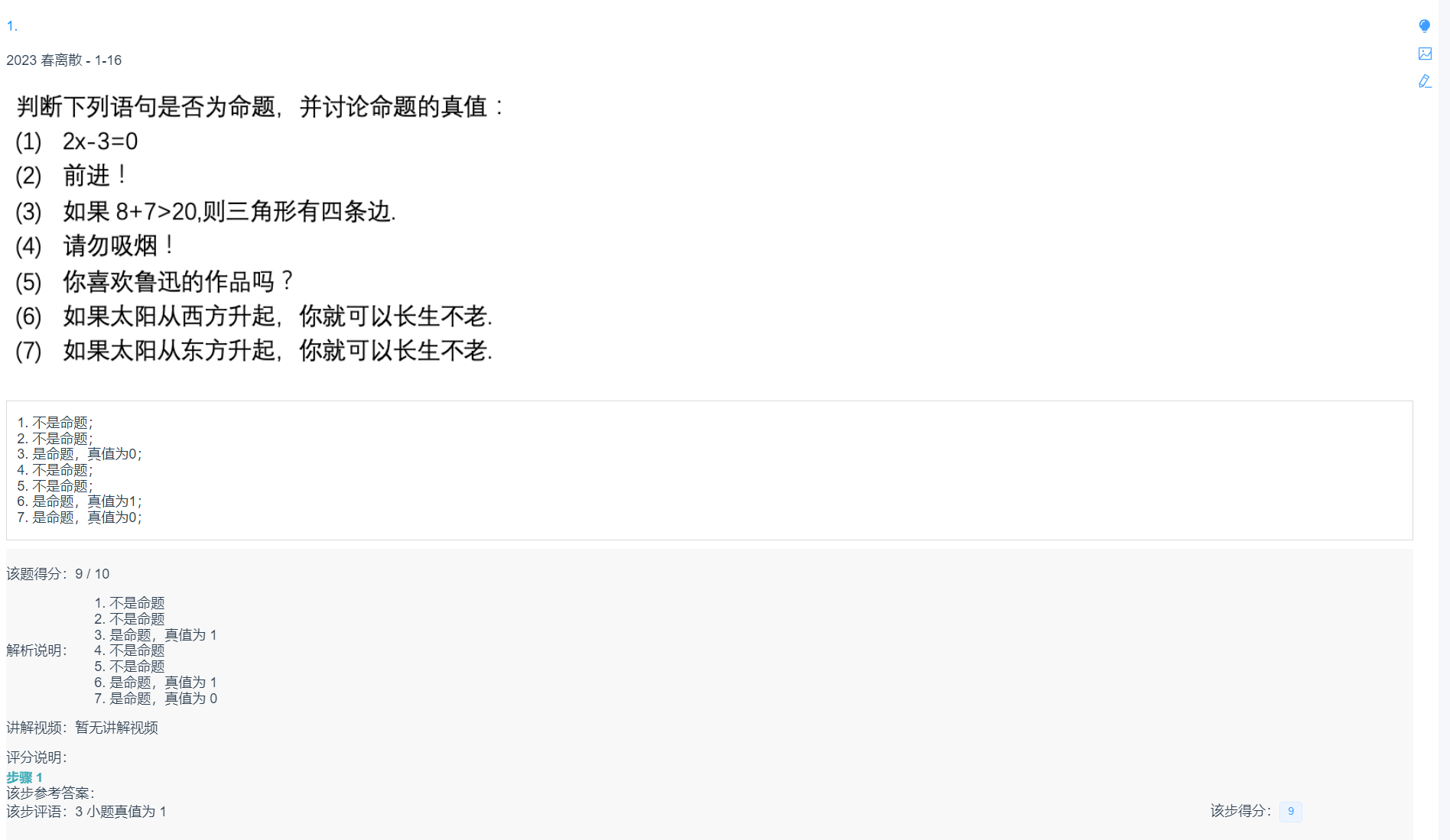
-
不是命题;
-
不是命题;
-
是命题,真值为0;
-
不是命题;
-
不是命题;
-
是命题,真值为0;
-
是命题,真值为0;
$2.2$

$$
\begin{align}
&1.\neg p\
&2.(\neg p)\wedge (\neg q)\
&3.p\oplus q\
&4.p\to q\
&5.p\to q\
&6.(p\wedge q)\to (r\vee s)\
&7.p\leftrightarrow (q \oplus r)\
&8.p\to q\
&9.p\to q\
&10.p\leftrightarrow q\
&11.\neg(p\vee q)\to r
\end{align}
$$

$2.3$

- 永真式
- 可满足式
- 可满足式
- 永真式
- 永真式
- 永假式
- 永真式

$2.4$
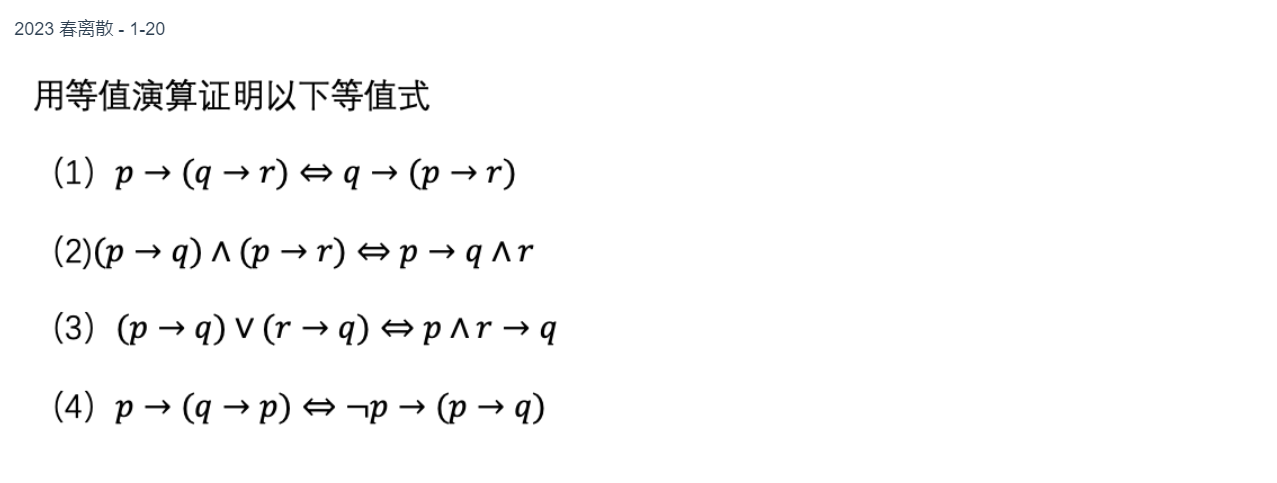
$$
\begin{align}
(1)\
&p\to (q\to r)\
\iff &\neg p\vee(\neg q\vee r)\
\iff &(\neg p \vee \neg q)\vee r\
\iff &(\neg q \vee \neg p)\vee r\
\iff &\neg q \vee (\neg p\vee r)\
\iff &\neg q \vee (p\to r)\
\iff &q\to(p\to r)\
(2)\
&(p\to q)\wedge(p\to r)\
\iff&(\neg p\vee q)\wedge(\neg p\vee r)\
\iff&\neg p \vee (q\wedge r)\
\iff&p\to q\wedge r\
(3)\
&(p\to q)\vee(r\to q)\
\iff&(\neg p\vee q)\vee(\neg r \vee q)\
\iff&\neg p\vee\neg r\vee (q\vee q)\
\iff&\neg p\vee\neg r\vee q\
\iff&\neg(p\wedge r)\vee q\
\iff&p\wedge r \to q\
(4)\
&p\to (q \to p)\
\iff&\neg p \vee (\neg q \vee p)\
\iff&(\neg p\vee p)\vee \neg q\
\iff&1\vee \neg q\
\iff&1\
同时又有&\neg p \to (p\to q)\
\iff&\neg \neg p \vee (\neg p \vee q)\
\iff&(p\vee \neg p)\vee q\
\iff&1\vee q\
\iff&1\
&二者均为永真式,且等值与1,故有二者等值
\end{align}
$$

$2.5$

$$
\begin{align}
(1)\
&易知(q\to r)\iff (\neg r\to\neg q)\
&由替换实例进行替换\
&有(Q\to R)\iff (\neg R\to\neg Q)\
(2)\
&(p\wedge q)\to r\
\iff&\neg(p\wedge q)\vee r\
\iff&\neg p\vee \neg q\vee r\
\iff&\neg p\vee(\neg q\vee r)\
\iff&\neg p\vee(q\to r)\
\iff&p\to(q\to r)\
&由替换实例进行替换\
&有(P\wedge Q)\to R\iff P\to(Q\to R)
\end{align}
$$
$2.6$
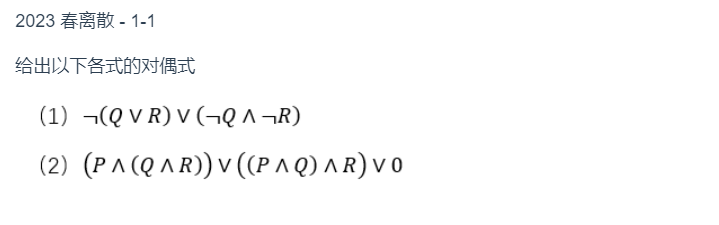
$$
\begin{align}
(1)\
&\neg(Q\wedge R)\wedge (\neg Q \vee \neg R)\
(2)\
&(p\vee(Q\vee R))\wedge((P\vee Q)\vee R)\wedge 1
\end{align}
$$
$2.7$

$$
\begin{align}
&由对偶定理\
(1)\
&A是永真式,则取R为1,R^为0\
&有A\iff R&\
&故A^\iff R^\
&即A^ \iff 0\
&故A为永假式\
(2)\
(1)\
&A是永假式,则取R为0,R^为1\
&有A\iff R&\
&故A^\iff R^\
&即A^ \iff 1\
&故A为永真式\
\end{align}
$$

第二次作业
$\text{1.1}$

$$
\begin{align}
(1)\
&(q\to p)\wedge(\neg p \to q)\leftrightarrow \neg p\
\iff&(\neg q \vee p)\wedge(\neg(\neg p) \vee q)\leftrightarrow\neg p\
\iff&(\neg q \vee p)\wedge(q\vee p)\leftrightarrow\neg p\
\iff&(\neg q \wedge q)\vee p \leftrightarrow\neg p\
\iff&p\leftrightarrow \neg p\
\iff &0\
&该公式通过真值演算等值于0,故该公式为永假式\
(2)\
&(p\to q)\wedge(q\to r)\wedge\neg(p\to r)\
\iff&(\neg p \vee q)\wedge(\neg q \vee r)\wedge\neg(\neg p \vee r)\
\iff&(\neg p \vee q)\wedge(\neg q \vee r)\wedge(p\wedge \neg r)\
\iff&((\neg p \vee q)\wedge p)\wedge((\neg q \vee r)\wedge \neg r)\
\iff&((\neg p \wedge p ) \vee(q \wedge p))\wedge((\neg q \wedge r)\vee (r \wedge \neg r)) \
\iff&(0 \vee(q \wedge p))\wedge((\neg q \wedge r)\vee 0)\
\iff&(q\wedge p)\wedge (\neg q \wedge r)\
\iff&p \wedge (q\wedge \neg q)\wedge r\
\iff&p\wedge 0 \wedge r\
\iff&0\
&该公式通过真值演算等值于0,故该公式为永假式\
\end{align}
$$

$\text{1.2}$

$$
\begin{align}
(1)
&\neg(\neg p \wedge \neg q)\vee \neg (\neg p \vee q)\
\iff&(p\wedge q)\vee (p\wedge \neg q)\
\iff&p\wedge (q\vee \neg q)\
\iff&p\
&故即证该等值式,由对偶定理有\
&\neg (\neg p\wedge \neg q)\wedge \neg (\neg p\wedge q)\iff p\
(2)
&(p\vee \neg q)\wedge(p\vee q)\wedge(\neg p \vee \neg q)\
\iff&p\vee (\neg q \wedge q)\wedge (\neg p \vee \neg q)\
\iff&(p\wedge \neg p)\vee(p \wedge \neg q)\
\iff&\neg (\neg p \vee q)\
&故即证该等值式,由对偶定理有\
&(p\wedge \neg q)\vee (p\wedge q)\vee(\neg p \wedge \neg q)\iff\neg (\neg p \wedge q)
\end{align}
$$

$\text{1.3}$

$$
\begin{align}
&1.{0,\to}\
&首先我们有{\neg ,\to }为极小完全集\
&又由于\neg p \iff p\to 0\
&故{\neg ,\to }是完全集\
&同时只含0的集合,无法表示真值赋值v(A) = 1\
&(其中A为只含命题变元p而不含其他命题变元的公式,取v(p/0)),而v(\neg p) = 1,即此时无法表示\neg\
&而只含\to 的集合,无法表示真值赋值v(A) = 0\
&(其中A为只含命题变元p而不含其他命题变元的公式,取v(p/1)),而v(\neg p) = 0,即此时无法表示\neg\
&即任意去掉一个后均不能构成完全集,故该集合为极小完全集\
&2.{\oplus ,\to}\
&首先我们有{\neg ,\to }为极小完全集\
&又由于\neg p \iff p\oplus (p\to p)\
&故{\oplus,\to}是完全集\
&又同时只含\oplus的集合,无法表示真值赋值v(A) = 1\
&(其中A为只含命题变元p而不含其他命题变元的公式,取v(p/0)),而v(\neg p) = 1,即此时无法表示\neg\
&而只含\to 的集合,无法表示真值赋值v(A) = 0\
&(其中A为只含命题变元p而不含其他命题变元的公式,取v(p/1)),而v(\neg p) = 0,即此时无法表示\neg\
&即任意去掉一个后均不能构成完全集,故该集合为极小完全集\
&3.{\oplus,\wedge,\leftrightarrow}\
&首先我们有{\neg ,\wedge }为极小完全集,而且{\oplus,\leftrightarrow}不是完全集(书上的例题应该可以用吧)\
&又由于\neg p \iff p\oplus (p\leftrightarrow p)\
&故{\oplus,\wedge,\leftrightarrow}是完全集\
&又同时只含{\oplus,\wedge}的集合,无法表示真值赋值v(A) = 1\
&(其中A为只含命题变元p而不含其他命题变元的公式,取v(p/0)),而v(\neg p) = 1,即此时无法表示\neg\
&只含{\wedge,\leftrightarrow} 的集合,无法表示真值赋值v(A) = 0\
&(其中A为只含命题变元p而不含其他命题变元的公式,取v(p/1)),而v(\neg p) = 0,即此时无法表示\neg\
&即任意去掉一个后均不能构成完全集,故该集合为极小完全集\
&4.{\oplus,\vee,\leftrightarrow}\
&首先我们有{\neg ,\vee }为极小完全集,而且{\oplus,\leftrightarrow}不是完全集\
&又由于\neg p \iff p\oplus (p\leftrightarrow p)\
&故{\oplus,\vee,\leftrightarrow}是完全集\
&又同时只含{\oplus,\vee}的集合,无法表示真值赋值v(A) = 1\
&(其中A为只含命题变元p而不含其他命题变元的公式,取v(p/0)),而v(\neg p) = ,即此时无法表示\neg\
&只含{\vee,\leftrightarrow} 的集合,无法表示真值赋值v(A) = 0\
&(其中A为只含命题变元p而不含其他命题变元的公式,取v(p/1)),而v(\neg p) = 0,即此时无法表示\neg\
&即任意去掉一个后均不能构成完全集,故该集合为极小完全集\
\end{align}
$$

$\text{1.4}$

$$
\begin{align}
&1.{\wedge, \vee, \to ,\leftrightarrow}\
&该集合无法表示真值赋值v(A) = 0\
&(其中A为只含命题变元p而不含其他命题变元的公式,取v(p/1)),而v(\neg p) = 0,即此时无法表示\neg\
&故该集合不是完全集\
&2.{\wedge,\vee,\oplus}\
&该集合无法表示真值赋值v(A) = 1\
&(其中A为只含命题变元p而不含其他命题变元的公式,取v(p/0)),而v(\neg p) = 1,即此时无法表示\neg\
&故该集合不是完全集\
\end{align}
$$

$\text{1.5}$
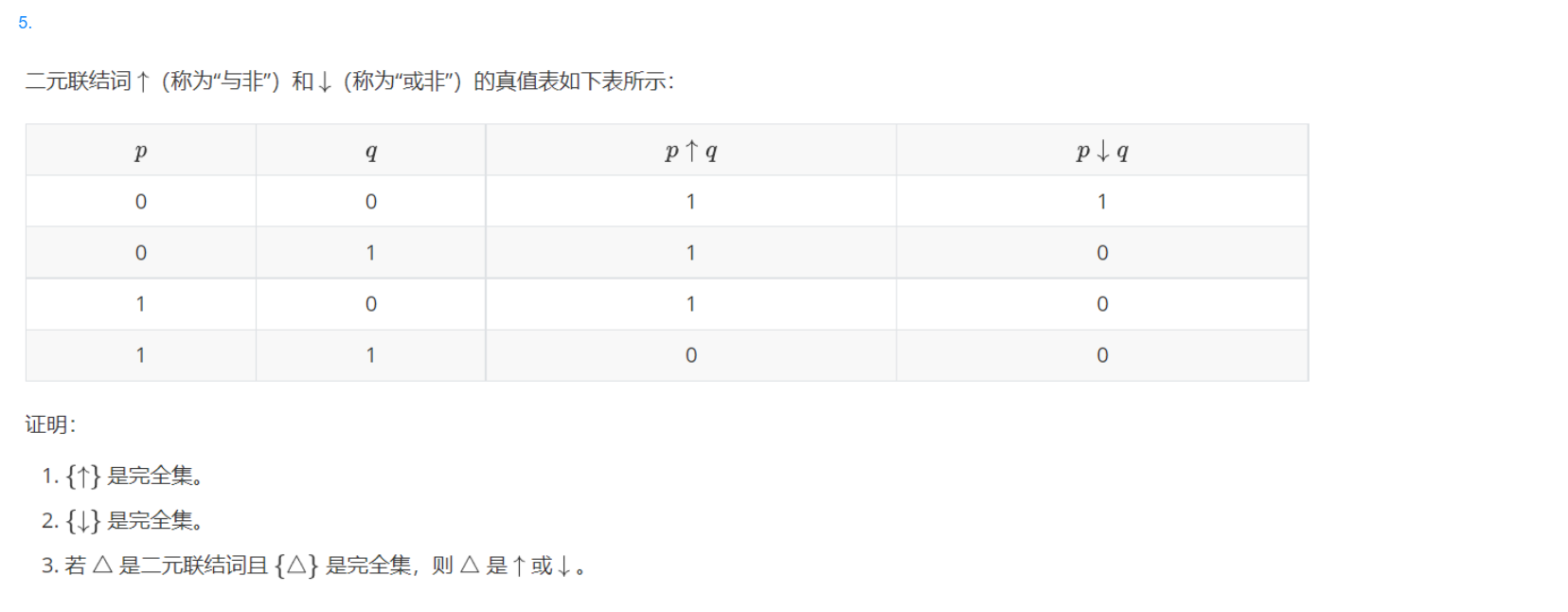
$$
\begin{align}
1.\
&{\uparrow}是完全集\
&首先我们知道{\neg,\wedge}是完全集\
&且有\neg p \iff p \uparrow p\
&p \wedge q\iff \neg(p \uparrow q)\iff(p \uparrow q)\uparrow(p \uparrow q)\
&故即证该集合为完全集\
2.\
&{\downarrow}是完全集\
&首先我们知道{\neg,\vee}是完全集\
&且有\neg p \iff p \downarrow p\
&p \vee q\iff \neg(p \downarrow q)\iff(p \downarrow q)\downarrow(p \downarrow q)\
&故即证该集合为完全集\
3.\
&{\Delta}为完全集\
&首先若有0 \Delta 0 = 0,或者1 \Delta 1 = 1\
&即0 \Delta 0 = 1,且1 \Delta 1 =0\
&那么\Delta无法表示\neg \
&又类似{\oplus,\leftrightarrow},若1\Delta0\neq 0\Delta 1\
&则仅含p,q两个命题变元而不含其他命题变元的公式A的真值情况中1的个数一定是偶数个\
&故该集合无法表示\wedge,\vee\
&于是\
&若1\Delta0=0\Delta1=0,则此时\Delta 即为\downarrow\
&若1\Delta0=0\Delta1=1,故此时\Delta即为\uparrow\
&综上即可得证
\end{align}
$$

$\text{1.6}$

def solve_formula(exp: str):
variables = {}
var_list = []
operations = {'or', 'and', 'not', '(', ')', 'True', "False"}
exp = ' ( '.join(exp.split('('))
exp = ' ) '.join(exp.split(')'))
tokens = exp.split()
for t in tokens:
if t not in operations and t not in variables:
variables[t] = None
var_list.append(t)
has_true = False
has_false = False
lim = 1 << len(var_list)
for i in range(lim):
for b in range(len(var_list)):
if i & (1 << b) != 0:
variables[var_list[b]] = 'True'
else:
variables[var_list[b]] = 'False'
const_exp = " ".join(list(map(lambda x: variables[x] if x in variables else x, tokens)))
if eval(const_exp):
has_true = True
else:
has_false = True
if not has_false:
return '永真式'
elif not has_true:
return '永假式'
else:
return '可满足式'
s = input("请输入一个合式公式,命题变元最多有p,q,r三个,仅包含与、或、非三种运算,用and,or,not来表示: ")
result = solve_formula(s)
print(result)
第三次作业
draft
$$
\begin{align}
&p \lfa q\
\iff&(p\to q)\w(q\to p)\
\iff&(\n p \v q)\w(\n q \v p)\
\iff&((\n p \v q) \w \n q)\v((\n p \v q) \w p)\
\iff&(\n p\w \n q)\v(q \w \n q)\v (\n p \w p)\v(q\w p)\
\iff&(p\w q)\v(\n p\w \n q)\
&( p\v q\v r)\w( p\v q\v\n r)\w( p\v\n q\v r)\w( p\v\n q\v\n r)\
&\w( p\v q\v r)\w(\n p\v q\v\n r)\w(\n p\v\n q\v r)\w(\n p\v\n q\v\n r)\
\end{align}
$$

$\text{1.1}$

$$
\begin{align}
&析取范式:\
&p,p\vee q,p\wedge \neg r,p\vee \neg p;\
&合取范式:\
&p,(p\vee q)\wedge r,p\wedge \neg r.p\vee \neg p;
\end{align}
$$

$p \vee q也是合取范式$
$\text{1.2}$
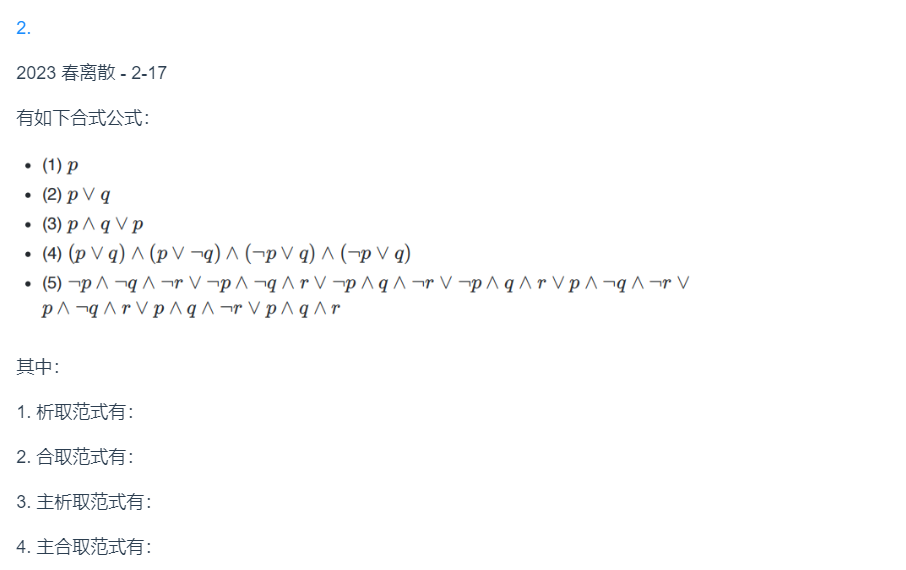
$$
\begin{align}
&1.析取范式有:\
&(1),(2),(3),(5)\
&2.合取范式有:\
&(1),(2),(4)\
&3.主析取范式有:\
&(1),(5)\
&4.主合取范式有:\
&(1)
\end{align}
$$

$\text{1.3}$

$$
\begin{align}
(1)&\neg p \wedge q \to r\
\iff&\neg(\neg p \wedge q)\vee r\
\iff&p\vee \neg q\vee r\
&可知主合取范式为:p\vee \neg q\vee r\
&主析取范式为:(\neg p\wedge\neg q\wedge\neg r )\vee(\neg p\wedge\neg q\wedge r )\vee(\neg p\wedge q\wedge r )\vee( p\wedge\neg q\wedge\neg r )\
&\vee( p\wedge\neg q\wedge r )\vee( p\wedge q\wedge\neg r )\vee(p\wedge q\wedge r)\
&且该合式公式为可满足式\
(2)&(p\to q)\to r\
\iff&\neg(\neg p \vee q)\vee r\
\iff&(p\wedge q)\vee r\
\iff&(p\vee r)\wedge(q\vee r)\
\iff&(p\wedge(q\vee \neg q)\vee r)\wedge((p\vee \neg p)\wedge q\vee r)\
\iff&(p\vee q\vee r)\wedge(p \vee \neg q \vee r)\wedge (\neg p \vee q\vee r)\
&可知主合取范式为:(p\vee q\vee r)\wedge(p \vee \neg q \vee r)\wedge (\neg p \vee q\vee r)\
&主析取范式为:(\neg p \wedge \neg q \wedge r)\vee(\neg p \wedge q\wedge r)\vee(p \wedge \neg q \wedge r)\vee(p\wedge q\wedge \neg r)\v(p\w q\w r)\
&且该合式公式为可满足式\
(3)&\n p\v \n q\to (p\lfa \n q)\
\iff&\n (\n p \v \n q)\v (p \w \n q)\v(\n p \w q)\
\iff&(p \w q)\v (p \w \n q)\v(\n p \w q)\
&可知主析取范式为:(p \w q)\v (p \w \n q)\v(\n p \w q)\
&主合取范式:p\v q\
&且该合式公式为可满足式\
(4)&p\v(p\to q\v(\n q \to r))\
\iff&p \v(\n p \v q\v (\n(\n q)\v r))\
\iff&p \v(\n p \v q\v q\v r)\
\iff&1\
&可知主合取范式为:1\
&主析取范式为:(\n p\w\n q\w\n r)\v(\n p \w \n q \w r)\v(\n p \w q \w \n r)\v(\n p\w q\w r)\
&\v(p\w \n q \w \n r)\v(p\w \n q \w r)\v(p\w q\w \n r)\v(p\w q\w r)\
&且该合式公式为永真式\
(5)&(p\to q \w r)\w(\n p\to \n q\w \n r)\
\iff&(\n p\v(q\w r))\w(\n(\n p)\v(\n q\w \n r))\
\iff&(\n p \v q)\w(\n p \v r)\w(p\v \n q)\w(p\v \n r)\
\iff&((\n p \v q)\v(r\w \n r))\w(\n p \v(q\w \n q)\v r)\w((p\v \n q)\v(r\w \n r))\w(p\v(q\w \n q)\v \n r)\
\iff&(\n p \v q\v r)\w(\n p\v q\v \n r)\w(\n p\v q\v r)\w(\n p\v\n q\v r)\w(p\v\n q\v r)\
&\w(p\v \n q\v\n r)\w(p\v q\v \n r)\w(p\v \n q\v \n r)\
\iff&(\n p \v q\v r)\w(\n p\v q\v \n r)\w(\n p\v\n q\v r)\w(p\v\n q\v r)\w(p\v \n q\v\n r)\w(p\v q\v \n r)\
&可知主合取范式为:(\n p \v q\v r)\w(\n p\v q\v \n r)\w(\n p\v\n q\v r)\w(p\v\n q\v r)\w(p\v \n q\v\n r)\w(p\v q\v \n r)\
&主析取范式为:(p \w q \w r)\v(\n p\w \n q\w \n r)\
&且该合式公式为可满足式\
(6)&p\w q\w (\n p\v \n q)\
\iff&(p\w q\w \n p)\v(p\w q\w \n q)\
\iff&0\
&可知主析取范式为:0\
&主合取范式为:(p\v q)\w(p\v\n q)\w(\n p\v q)\w(\n p\v\n q)\
&且该合式公式为永假式\
\end{align}
$$
$\text{1.4}$

有,p既是关于p的主析取范式,又是关于p的主合取范式
$\text{1.5}$

$$
Q\v R,\n Q\vDash R
$$

$\text{1.6}$

def terms(exp: str) -> int:
variables = {}
var_list = []
operations = {'or', 'and', 'not', '(', ')'}
exp = ' ( '.join(exp.split('('))
exp = ' ) '.join(exp.split(')'))
tokens = exp.split()
for t in tokens:
if t not in operations and t not in variables:
variables[t] = None
var_list.append(t)
cnt_true = 0
cnt_false = 0
lim = 1 << len(var_list)
for i in range(lim):
for b in range(len(var_list)):
if i & (1 << b) != 0:
variables[var_list[b]] = 'True'
else:
variables[var_list[b]] = 'False'
const_exp = exp
for v in variables:
const_exp = const_exp.replace(v, variables[v])
if eval(const_exp):
cnt_true += 1
else:
cnt_false += 1
return cnt_false
def main():
print(terms(input()))
if __name__ == '__main__':
main()

