高代期末

线代期末串讲

https://bhpan.buaa.edu.cn/link/AA8158DA29E46E4B62A400D7DA65647D7C
文件夹名：高代期末串讲
有效期限：永久有效

资料如上

2023 12.31 胡健

线性代数这门课程的切入点有很多，这里从知识层面上划分出来了线性方程组和向量组，线性空间，矩阵与行列式这三大部分。同时，会讲到几个重要的定理和公式。

线性方程组和向量组

• 线性方程组

齐次解和非齐次解的讨论
$$
AX=O\
AX=\beta
$$
齐次：有唯一解，有无穷多组解

非齐次：无解，有唯一解，有无穷多组解
$$
有解\iff r(A)=r(A|\beta)
$$
可拓展到矩阵方程的解的情况

通解问题
$$
\begin{align}
&X=t_1\varepsilon_1+\dots t_p\varepsilon_p\
&X=t_1\varepsilon_1+\dots t_p\varepsilon_p + X_1
\end{align}
$$

• 向量组

(列向量组)
$$
\alpha_i\in R^n,{\alpha_1\dots \alpha_p}
$$
线性相关与线性无关的含义
$$
\begin{align}
&存在不全为0的k_1\dots k_p,k_1\alpha_1 +\dots k_p\alpha_p = 0\Rightarrow线性相关\
&k_1\alpha_1 +\dots k_p\alpha_p = 0\rightarrow k_1\dots k_p = 0\Rightarrow线性无关
\end{align}
$$

• 极大线性无关与秩

极大线性无关组指的是：
$$
\alpha_1\dots\alpha_m线性无关，且加上向量组中任一向量\alpha后线性相关
$$
向量组的秩的含义是极大线性无关组中向量的个数

• 向量组的等价

一个向量组A中的每一个向量可以用另一个向量组B来线性表示，称向量组A能由向量组B线性表示

向量组的等价指的是可以相互线性表示

• 向量组的一些性质

• 相关的线性表示（及其逆，单边法则）

由线性相关的定义可推出，其中某个向量可以由其余向量线性表示，这又可推出其中的某个向量可以写成前面的向量的线性组合。
所以我们逆过来看，线性无关，等价于
$每一个向量都不可由前面的向量表示（\alpha_i = 0） $
这我们叫做单边法则

• 大数法则/不大法则

我们先来看，一个向量组被另一个向量组表示被表示的意义。
$S_1组被S_2组表示\Leftrightarrow \forall \alpha_i \in S_1 , \alpha_i 可以被 \beta_j \in S_2 表示 $
大的向量组可以被小的向量组表示，大组必相关
（逆否命题：若A组无关，但可以被B组表示，则A比B小 ——不大法则）
为啥可以被表示，我们可以理解了后面的秩再来说，是不是说AX=B有解啊。

• 表示的传递性

$我们说S_2 能被S_1表示，S_1能被S_0表示，则S_2能被S_0表示$

• 唯一表示法则

${\alpha_1,……,\alpha_n}无关,{\alpha_1,……,\alpha_n,\beta}相关，则\beta 由{\alpha_1,……,\alpha_n}唯一表示 $

• 子组相关法则

子组相关，全组必定相关
proof:
$k_1\alpha_1 + k_2\alpha_2 +……+k_p\alpha_p = 0 (k_1,……,k_p不全为零) $
$\therefore k_1\alpha_1 + k_2\alpha_2 +……+k_p\alpha_p + 0\alpha_{p+1} + …… + 0\alpha_n = 0$

• 等数法则

${\alpha_1,……\alpha_p},{\beta_1,……\beta_q}两组无关，且能相互表示，则p=q $
由不大法则可证

• 长短法则

长相关则短相关，短无关则长无关
看具体怎么理解了，有的老师说“如果矩阵A的子矩阵A0的各行（列）线性无关，则由A0的这些行（列）扩充得到的A的行（列）线性无关。”
这是从大到小，从矩阵看问题
也可以这么理解（从小到大，从向量组）

• 行变再行变，列的关系不改变

空间(解空间，内积空间)

解空间(初次接触)

张成空间(你已经会很多了)

欧式空间(你会的差不多了)

线性空间(你会了！！)

• 定义

满足八条性质，其实就是满足封闭性和线性性

• 生成空间的定义

由向量组表示的所有向量的集合
$$
\begin{align}
&\alpha_1\dots\alpha_m\
&L={\lambda_1\alpha_1 \dots \lambda_m\alpha_m|\lambda_1\dots\lambda_m\in R}
\end{align}
$$

• 解空间的理解

定义：n元齐次线性方程组的解集是n维向量空间$F^n$的非空子集(易证满足封闭性和线性性)

生成空间角度：基础解的张成空间

矩阵内积的理解：
$$
(\alpha_1,\dots,\alpha_m)
\begin{pmatrix}
x_1\
\vdots\
x_m
\end{pmatrix}\
AX
$$

• 空间的交与和（还有直和和并，应该不考）

how to solve？

$V_1:\alpha_1\dots \alpha_p,V_2:\beta_1\dots\beta_q$

空间的交：
$$
\begin{align}
&\gamma = s_1\alpha_1+\dots s_p\alpha_p = t_1\beta_1+\dots t_q\beta_q\
&解出来后得到s_1\dots s_p\
&带入后易得
\end{align}
$$
空间的和：
$$
\begin{align}
&{\alpha_1\dots\alpha_p,\beta_1\dots\beta_q}这个向量组的极大线性无关组\
&和空间的维数即为极大线性无关组的秩
\end{align}
$$
维数公式
$$
\dim(W_1+W_2)=\dim W_1+\dim W_2-\dim (W_1\cap W_2)
$$
其中$W_1+W_2={w_1+w_2:w_1\in W_1,w_2\in W_2}$

• 内积与Gram矩阵

$$
\begin{align}
&A={\alpha_1\dots\alpha_n}\
&Gram=
\begin{pmatrix}
(\alpha_1,\alpha_1)&\dots &(\alpha_1,\alpha_n)\
\vdots & &\vdots\
(\alpha_n,\alpha_1) &\dots &(\alpha_n,\alpha_n)
\end{pmatrix}\
&Gram=A^TA
\end{align}
$$

定义预正交阵和正交阵

预正交阵：列向量两两正交

正交阵：两向量两两正交且每个列向量的模为1

度量阵：由基向量产生的Gram矩阵，特殊情况下是单位阵

二次型
$$
\begin{align}
&f=\sum_{i=1}^n\sum_{j=1}^na_{ij}x_ix_j\
&二次型对应的矩阵为：\
&\begin{pmatrix}
a_{11}&\dots &a_{1n}\
\vdots & &\vdots\
a_{n1} &\dots &a_{nn}
\end{pmatrix}\
&a_{ij}=a_{ji}
\end{align}
$$

• 线性映射和线性变换

线性映射：$R^n\rightarrow R^m$

线性变换：$R^n\rightarrow R^n$

这个概念挺抽象的

不同书定义也不一样(点名批评同济大学的紫书)

这里以《矩阵论》上面的定义为准

• 过渡矩阵与坐标变换公式

  若两组基$ S=\begin{bmatrix}{\varepsilon_1,\cdots,\varepsilon_n}\end{bmatrix}, T=\begin{bmatrix}{\eta_1,\dots,\eta_n}\end{bmatrix}$满足基变换公式$ T= S P$，则称$ P$是从$\S$到$ T$的过渡矩阵。

  设向量$\alpha$在$ S, T$下的坐标分别为$ X, Y$，则满足坐标变换公式$ X= P Y$。

• 线性变换矩阵

  对于一组基$\xi_1,\dots,\xi_n$，若存在矩阵$A$使得线性变换$\sigma$满足$\sigma(\xi_1,\dots,\xi_n)=(\xi_1,\dots,\xi_n) A$，则称矩阵$ A$为线性变换$\sigma$在基$\xi_1,\dots,\xi_n$下所对应的矩阵。

  若线性空间$V$的线性变换$\sigma$在两组基$\xi_1,\dots,\xi_n$以及$\eta_1,\dots,\eta_n$下对应的矩阵分别为$ A, B$，$\xi_1,\dots,\xi_n$到$\eta_1,\dots,\eta_n$的过渡矩阵为$ P$，则有$ B= P^{-1} A P$。

虽然这个也有点抽象，但是整理了一下也就这几个公式

理解不了就记住吧

矩阵与行列式

• 矩阵的可逆与正交

$$
\begin{align}
&A=A_{n\times n}\
&r(A)=n\
\iff&行满秩\
\iff&列满秩\
\iff&A^{-1}存在\
\iff&|A|\ne 0\
\iff&\lambda_i\ne 0|A|=\lambda_1\dots\lambda_n\
\end{align}
$$

正交：$A^T=A^{-1}$或者$A^TA^{-1}=A^{-1}A^T=I_n$

• 矩阵的秩

行秩：行向量组的秩

列秩：列向量组的秩

阶梯秩：化为阶梯阵后非零行的个数

古典秩：存在k阶子式的行列式不为0，任意k+1阶子式的行列式都为0

这四个是等价的

• 行列式的计算

这个我感觉高阶的也不会让你算

低阶的直接爆算或者化为上三角行列式

范德蒙德行列式

下降公式/换位公式

• 相伴秩公式

$$
A=A_{n\times n}\
A^*=
\begin{pmatrix}
A_{11} &A_{21}&\dots &A_{n1}\
\vdots &&&\vdots\
A_{1n} &A_{2n}&\dots &A_{nn}
\end{pmatrix}
$$

注意这里还转置了一下

$AA^*=|A|I_n$

可得$|A^*| = |A|^{n-1}$

和伴随矩阵有关的秩的公式
$$
r(A^*) =
\begin{cases}
n,r(A) = n\
1,r(A)=n-1\
0,else
\end{cases}
$$

proof:由古典秩的含义

第二个用到$AA^=O 有r(A)+r(A^) \le n $

且$r(A^*) \ge 1$

特征值与二次型

• 根的遗传公式

零化式

theory

• Cayley定理

• 许尔公式
• 相似对角化

可对角化

1. n阶矩阵A与对角阵相似（即A能对角化）的充分必要条件是A有n个线性无关的特征向量。
2. 如果n阶矩阵A的n个特征值互不相等，则A与对角阵相似。
3. 对称阵的特征值为实数
4. 不同特征根的特征向量正交

对称阵A对角化的步骤

1. 求出A的全部互不相等的特征值$\lambda_1,\dots \lambda_s$，它们的重数依次为$k_1,\dots k_s(k_1+\dots +k_s = n)$。

2. 对每个$k_i$重特征值$\lambda_i$，求方程$(A-\lambda_i I)X=O$的基础解系，得$k_i$个线性无关的特征向量。再把它们正交化、单位化，得ki个两两正交的单位特征向量。因$k_1+\dots +k_s=n$，故总共可得n个两两正交的单位特征向量。

$Schimidt$正交化方法

若有$n$个线性无关的向量$\alpha_1,\dots,\alpha_n$，则过程分为正交化和单位化

正交化过程
$$
\beta_k=\alpha_k-\sum_{i=1}^{k-1}\frac{(\beta_i,\alpha_k)}{(\beta_i,\beta_i)}\beta_i,\quad k=1,\dots,n
$$
单位化过程
$$
\eta_k=\frac{\beta_k}{||\beta_k||},\quad k=1,\dots,n
$$
从而得到一组单位正交向量$\eta_1\cdots,\eta_n$。

3. 把这n个两两正交的单位特征向量构成正交阵P，便有$P^{-1}AP = P^TAP = Λ$。注意Λ中对角元的排列次序应与P中列向量的排列次序相对应。

• 实对称阵的性质

实对称矩阵的正交相似对角化

（1）实对称矩阵的特征值均为实数；

（2）实对称矩阵对应不同特征值的特征向量相互正交；

（3）实对称矩阵必定可以相似对角化；

（4）若$ A$是$n$阶实对称矩阵，且特征值为$\lambda_1,\cdots,\lambda_n$，则存在正交矩阵$ Q$，使得
$$
Q^T A Q=\begin{bmatrix}\lambda_1&&\&\ddots\&&\lambda_n\end{bmatrix}
$$
（5）若$ A$和$ B$均为$n$阶实对称矩阵，则$ A$和$ B$相似的充要条件是$ A$和$ B$有相同的特征值。

• 二次型与六二条件

正定矩阵：

（1）$ A$所有特征值均为正;

（2）$ A$正惯性指数为$n$；

（3）$ A$与单位阵合同；

（4）$ A$的各阶顺序主子式大于零；

（5）存在可逆矩阵$ P$使得$ A= P^T P$。

（6）若对任意$n$维维非零向量$ \alpha$均有$\alpha^T A\alpha>0$

负定矩阵：

（1）若对任意$n$维维非零向量$ \alpha$均有$\alpha^T A\alpha<0$

（2）$ A$的奇数阶主子式为负，偶数阶主子式为正；

• 双合同定理

若$A,B$同阶实对称，其中一个为正定，可设$A$正定，存在可逆$W$,$W^TAW=I_n，W^TBW=diag(d_1,\dots,d_n)$,即$W^TAW,W^TBW$都为对角形

more

一些典型的整理

• 秩公式

阶梯阵概念，及其与向量组秩的联系。

矩阵就是向量组拼起来的，所以矩阵的秩就是向量组的秩。
我们在线性方程组的矩阵消元法中见识过，我们把一个矩阵变成阶梯状，我们考虑一下，变成阶梯状以后，后面的向量前缀都是零，所以不可能可以表示前面的向量，所以很简单，阶梯有多少阶，就会有多少秩。
那么到底是行向量的秩还是列向量的秩呢，不用纠结我们通过阶梯可以看出，行向量的秩就是列向量的秩。
所以三种同解变形，其实就代表着三种初等变换。

秩一阵

我们来看一个矩阵，秩一阵，可分解为两个向量之间的乘积。

我们在最后再来谈秩的各种公式的关系

• 满秩则有唯一解
  $proof: \because r(A) = n $
  $\therefore {\alpha_1,……,\alpha_n}可作为一组基 $
  $\therefore \forall \beta \in R^n 都会存在\beta 的坐标(x_1,……,x_n) $
  $坐标即为唯一解 $
• 满秩则可逆
  $proof: 由上可知：AX_1 = \varepsilon_1, AX_2 = \varepsilon_2,……,AX_n = \varepsilon_n 都有解$
  $所以AA^{-1} = I可解出A^{-1} = (X_1,X_2,……,X_n) $

所以说到这就只需要明确一个事情，满秩，行向量组列向量组无关，行列式不等于0，可逆，只有唯一解，非奇异这都是等价的概念

分块秩公式

$$
r\begin{pmatrix}
A &O\
O &B
\end{pmatrix}=r(A)+a(B)\
r\begin{pmatrix}
O &B\
A &O
\end{pmatrix}=r(A)+a(B)\
r\begin{pmatrix}
A &C\
O &B
\end{pmatrix}\ge r(A)+a(B)\
$$

乘积不增秩公式

$$
\begin{align}
&r(AB)\le r(A),r(B)\
&A=A_{m\times n} = (\alpha_1,\dots,\alpha_n),B=B_{n\times p} = (\beta_1,\dots,\beta_p)\
&AB=(A\beta_1,\dots,A\beta_p)\
&A\beta_i=\alpha_1b_1+\dots+\alpha_nb_n,\beta_i=\begin{pmatrix}
b_1\b_2\\vdots\b_n
\end{pmatrix}\
&AB可以被{\alpha_1,\dots,\alpha_n}表示
\end{align}
$$

积0公式

$$
\begin{align}
&AB=O\
&r(A)+r(B)\le n
\end{align}
$$

转置积秩公式

$$
r(A)+r(B)\le r(AB)+n
$$

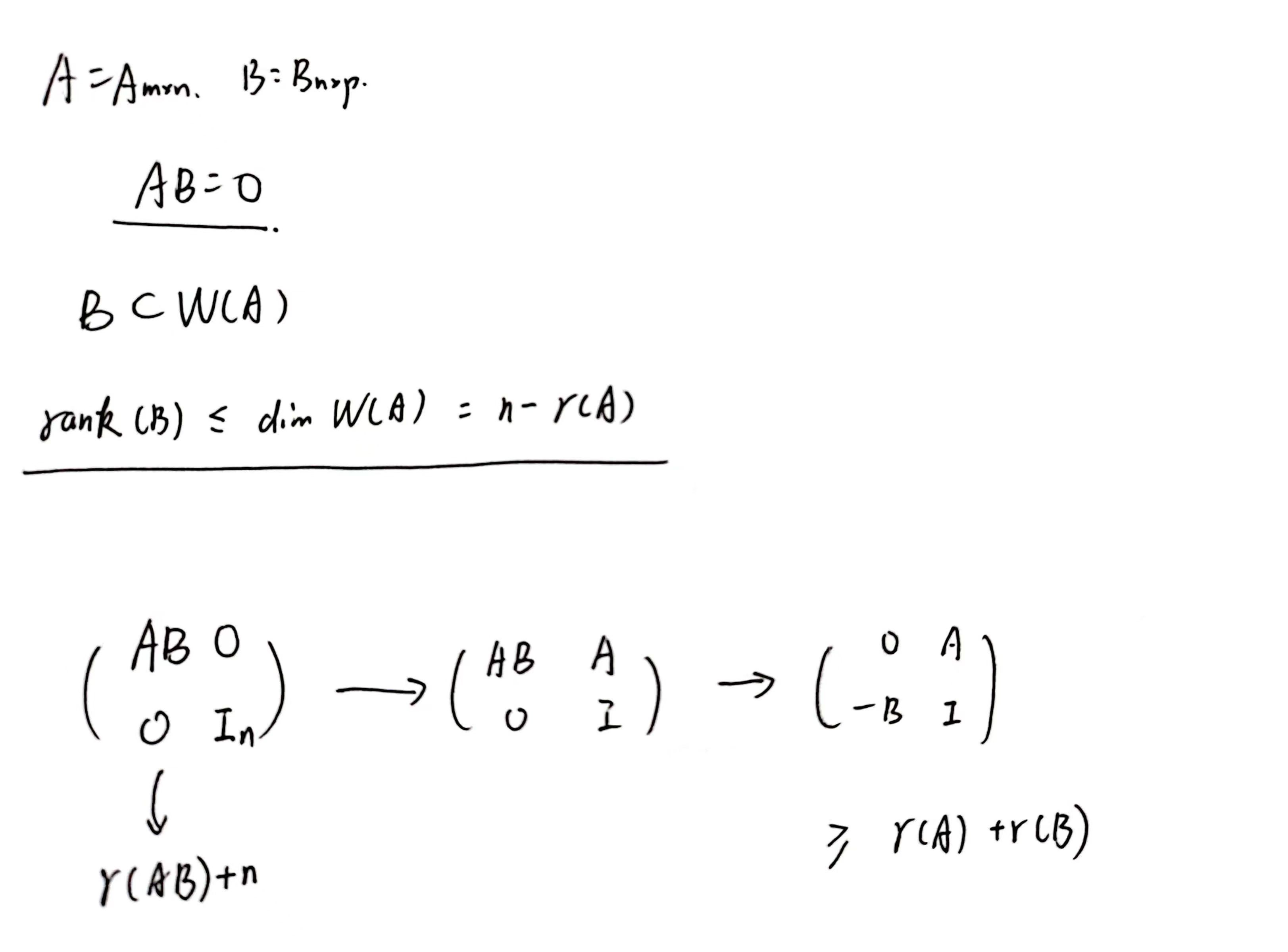
加减秩公式

$$
\begin{align}
&r(A+B)\le r(A)+r(B)\
&r(A-B)\le r(A)+r(B)\
&r(A+B)=r(A|B)r\begin{pmatrix}I_n\I_n\end{pmatrix}\le r(A|B)\le r(A)+r(B)
\end{align}
$$

• 可逆的等价表示

1. $A$的行列式不等于0

2. $A$的秩等于$n$，即$A$为满秩矩阵

3. $A$的行（列）向量组线性无关

4. 齐次方程组$Ax=0$只有零解

5. 对于任意$b$属于$R^n$(表示向量空间)，Ax=b总有唯一解

6. A与单位矩阵等价

7. A可表示成若干个初等矩阵的乘积

8. A的列向量可以作为n维向量空间$R^n$的一组基

9. $R^n$中任意一个向量都可以由$A$的列向量线性表出

10. $A$的特征值全不为0

11. $A^TA$是正定矩阵

12. $A$是非奇异的

• 求逆的方法学

初等变换（常用且方便）

伴随矩阵法

分块矩阵法

零化式法

• 下降公式